Una guía para exorcistas (Parte III): ¡Vade retro Satanás!

 

"At quite uncertain times and places/The atoms left their heavenly path/And by fortuitous embraces/Engendered all that being hath./And though they seem to cling together/And form 'associations' here/Yet, soon or late, they burst their tether/And through the depths of space career.

En tiempos y lugares bastante inciertos/Los átomos abandonaron su camino celestial/Y por abrazos fortuitos/generaron todo esto que hay./Y a pesar de que parecen aferrarse a estar juntos/Y formar 'asociaciones' aquí/Aun así, tarde o temprano, romperán su lazo/Y recorrerán las profundidades del espacio." 

James Clerk Maxwell - Molecular Evolution

Nada mejor que empezar con un poema de un científico para afrontar esta entrada tan especial del blog. Ha llegado el momento decisivo, la culminación del debate acerca de si el diablillo de Maxwell tal y como lo hemos definido (esto es, tal y como la física clásica lo definió) puede tener una existencia real o bien podemos deshacernos de él con un argumento incuestionable, robusto como ninguno. Si aún no has leído las entradas anteriores o crees que necesitas repasarlas (recomendable en todo caso), visita la primera parte de la guía para comprender un poquito mejor la Física clásica y la segunda entrada cuando estés listo para adentrarte en el espacio de fases y el equilibrio termodinámico.

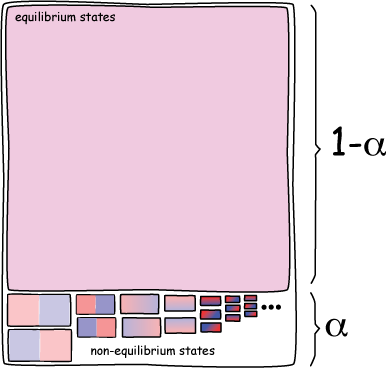
Vamos al lío. Dije que los estados de equilibrio son los más probables para un sistema porque contienen un número muy elevado de configuraciones diferentes; el cociente entre todas las posibilidades de equilibrio y las totales que puede haber es muy superior que la razón entre las posibilidades de no-equilibrio y el global. Esto nos lleva a determinar que en el espacio de fases la mayoría de estados accesibles por el gas con bolitas moviéndose será de equilibrio. Dicho de otra manera, los estados de equilibrio ocupan la inmensa mayoría del espacio de fases. A la porción del espacio de fases (conjunto de todos los puntos de dicho espacio que simbolizamos con V) donde el sistema se encuentra en no-equilibrio lo llamaremos α, mientras que 1-α corresponde a la región del espacio de fases ocupado por los estados de equilibrio del gas. Nótese en el esquema de la figura la enorme diferencia de tamaño entre ambas regiones (no está a escala porque los estados de no-equilibrio serían casi invisibles).

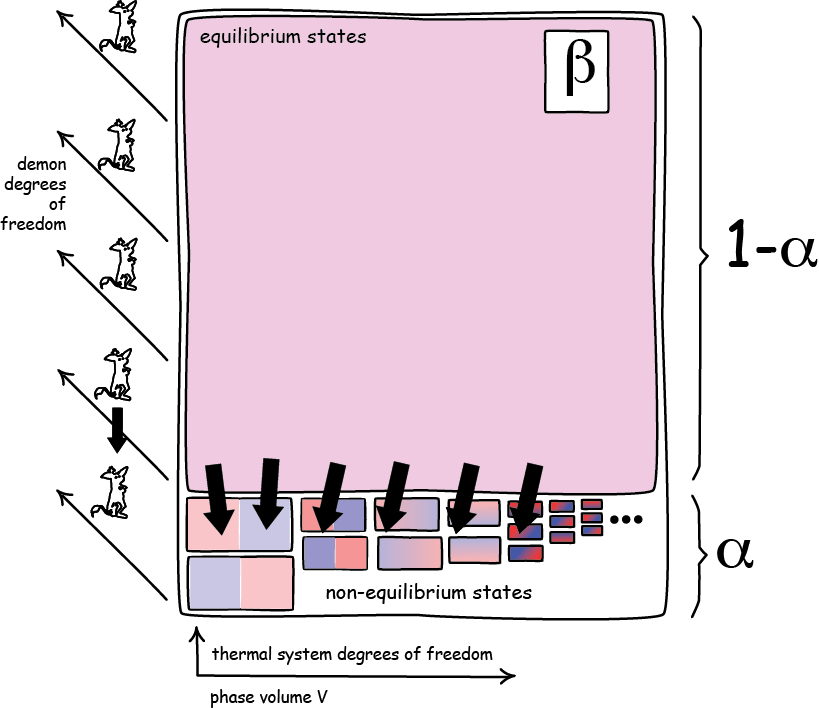
Recordemos que el diablillo actuaba sobre el gas a partir de que éste se encontrase en equilibrio (los dos compartimentos se encontraban a la misma temperatura; había una homogeneidad de velocidades de las bolitas entre un lado y otro del sistema). Por lo tanto, la pretensión del diablillo consiste en llevar al sistema hacia un en la región del espacio de fases correspondiente al no-equilibrio, cuyo volumen es αV (la fracción de no-equilibrio multiplicada por el volumen total del espacio). Supongamos que el ente diabólico logra actuar sobre todos los estados de equilibrio salvo una pequeña fracción que denominaremos β (nada es perfecto en este mundo ni en el infernal). Esto supondría que el volumen del espacio de fases del gas sobre el que actúa el diablillo es: (1-α)(1-β)V.

Ahora bien, el diablillo también ocupa una parte del espacio de fases que caracterizamos por el volumen v que, si bien no es cero, es mucho menor que V porque tiene muchos menos grados de libertad que el gas (muchas menos estados posibles). Es necesario considerar este aspecto porque el sistema bajo estudio consiste en el conjunto que formn el gas Y el diablillo, ya que sin su acción resultaría imposible (a priori) que la transformación se llevase a cabo, luego olvidarnos de su presencia para este razonamiento sería un descuido. Por lo tanto, en el espacio de fases del sistema completo, se produce una compresión entre un volumen inicial v(1-α)(1-β)V y otro final vαV. Sabemos que el volumen final es menor que el inicial porque apuntamos previamente que αV era muy pequeño por ser de no-equilibrio y que, por ser muy eficiente, el diablillo actuaba sobre casi la totalidad de estados de equilibrio, dejándose solo un número β muy pequeño en el tintero. El efecto neto es:

 vαV < v(1-α)(1-β)V

La estocada definitiva al diablillo viene de la mano del Teorema de Liouville. Esta ley demostrada matemáticamente para sistemas clásicos como el nuestro establece que el volumen del espacio de fases de un sistema no se puede comprimir durante ninguna evolución temporal. En otras palabras, la desigualdad que hemos escrito antes no puede suceder con las premisas sobre las que hemos sustentado la argumentación del sistema (gas + diablillo). ¡El diablillo queda exorcizado! No me negarán que la manera de acabar con la molesta presencia del diablo no es elegante y gratificante; no hemos necesitado crucifijos, ni agua, ni cuerdas para atar a gente a la cama, etc. 

La discusión sobre este experimento mental resulta recurrente en la/s asignatura/s de Termodinámica y Estadística en los grados en Física o en los cursos similares de Química. Se han propuesto distintas soluciones al problema a lo largo del último siglo, desde las más extravagantes hasta las más comunes que tienen que ver, generalmente, con el Segundo Principio de la Termodinámica y sus consecuencias (entropía). Estas últimas demostraciones tienden a asumir que, puesto que esta regla fundamental de la Naturaleza se cumple, no resulta posible actuar sobre el gas para separar las partículas según su velocidad sin producir por ningún lado una energía residual en forma de calor que resulte inutilizable y se compute como pérdida. El problema con la asunción del Segundo Principio es que trae problemas de circularidad en las soluciones basadas en la denominada Teoría de la Información (con circularidad me refiero a que una pescadilla que se muerde la cola: postulados que involucran conclusiones). Por otra parte, cuando no se asume la validez del Segundo Principio, muchas veces se pretende utilizar como excusa la entropía (próximamente trataré de explicar qué diantres es eso, si bien ya existen entradas relacionadas con ella en el blog Sapere Aude) para caer en una zanja poco señalizada: la entropía termodinámica se define a partir del Segundo Principio, luego obviarlo deja sin sentido a la magnitud. 

Quiero despedirme de esta sección aprovechando para recomendar la web del Profesor John D. Norton de la Universidad de Pittsburg, donde encontré esta demostración y otras tantas explicaciones cuando me topé con ella una tarde aburrida de tercero de carrera. No voy a negar que son generalmente explicaciones de fenómenos nada triviales, pero ¿por qué no intentarlo si sienten curiosidad? Por supuesto, si te han quedado dudas o quieres compartir algo, déjalo en comentarios.

¡Nos vemos diablillos!