Una guía para exorcistas (Parte II): el espacio de fases y los estados de equilibrio.

 

"Preferiría tener preguntas sin respuesta a tener respuestas incuestionables / I would rather have questions that can't be answered that answers that can't be questioned" 

Richard Feynman

Proseguimos, diablillos, con la publicación del manual para exorcizar al Diablillo de Maxwell. En la primera parte expliqué los principios básicos de la Física clásica y el enfoque hamiltoniano como manera particular de trabajar. Te aconsejo que des un repaso por el texto para refrescar las ideas frente a lo que se viene a continuación.

En esta segunda parte no trataremos con ninguna ecuación en el razonamiento del exorcismo (sí las usaremos en un ejemplo complementario). Esto no significa que debas relajarte, sino todo lo contrario; vienen curvas peligrosas cargadas de conceptos físico-matemáticos nada triviales. Abróchate el cinturón y abre tu cerebro porque viene un café bien cargado.

El sistema (tanto el diablillo como el gas) descrito en la Introducción y en la primera parte de esta guía está gobernado por la Física clásica. Eso significa que existe una función hamiltoniana con la que se pueden obtener las variables fundamentales de posición y momento lineal, i.e., el estado del sistema. Por aquello de no complicarnos la vida demasiado (ya dije que los físicos somos bastante simples en algunas cosas) vamos a hacer una última asunción acerca del sistema: la evolución temporal del sistema viene dada por un hamiltoniano invariante bajo inversión temporal e independiente del tiempo. "¿Qué diantres es eso?" ¡Vaya, pequeño Timmy, parece que no tuviste suficiente la última vez! Que una función como es nuestro querido hamiltoniano sea invariante bajo inversión temporal supone que es equivalente tanto en un instante de tiempo llamado t como en su opuesto -t. Generalmente, las leyes macroscópicas del universo no cumplen esta propiedad debido a una tendencia natural a evolucionar hacia determinados estados, pero nuestro sistema sí se comporta adecuadamente (esperad unas líneas y descubriréis por qué). Por otro lado, pequeño Timmy, la independencia respecto del tiempo implica ir un paso más allá y concebir que el sistema no sigue una historia que cambie su manera de proceder; da igual cuándo empiece el diablo a separar las pelotitas del gas porque su efecto será el mismo. Vuelve a leer estas líneas y, si sigues con dudas, pregúntame en comentarios.

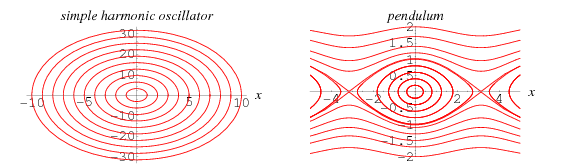
Así pues, vamos a tirar del hilo de la frase con la que despedí la primera entrada. Muy probablemente hayas visto en algún momento de tu vida escolar una sección llamada "Tiro parabólico" donde describe el movimiento de una bala que sale disparada, en ausencia de aire, y te piden calcular el lugar del impacto o la altura máxima que alcanza. La trayectoria que sigue el proyectil en el plano x-y que nos describe el sistema es la de una parábola invertida (vértice como punto más alto en el eje y; el suelo se suele tomar tradicionalmente como eje x). Cabría preguntarse, ¿existe otra representación más rica físicamente que la del espacio ordinario? La respuesta es SÍ. Se denomina espacio de fases al espacio matemático compuesto por las posiciones y momentos lineales de un sistema físico. En lugar de trabajar con trayectorias en un plano del espacio ordinario, la mecánica clásica desde el punto de vista hamiltoniano permite generar nuevas maneras de estudiar los sistemas físicos clásicos a partir de sus indicadores fundamentales (posición y momento), de manera que se puede observar su evolución temporal mediante las trayectorias que siguen entre los puntos de este espacio de fases, que representan estados del sistema. La solución de las ecuaciones de Hamilton determina sobre qué puntos pasa la trayectoria del espacio de fases, i.e., qué estados puede alcanzar el sistema durante la evolución temporal. Para que reflexiones sobre lo anterior, te presento el diagrama de fases del oscilador armónico simple, una masa m sujeta a un muelle de masa despreciable, y del péndulo simple, una bola de masa m atada a una cuerda tremendamente ligera. El eje horizontal representa las posiciones x, mientras que el vertical corresponde a los momentos lineales p (las unidades aquí no nos importan). Las distintas trayectorias, líneas continuas de color rojo, dependen de las condiciones iniciales del sistema (posición y momento al comenzar el movimiento).

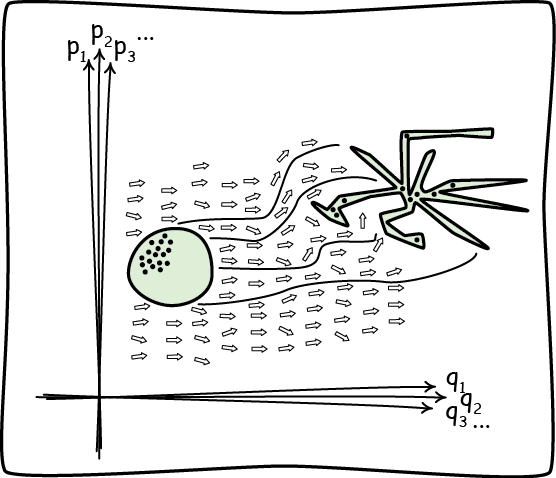
El espacio de fases tiene una serie de reglas inquebrantables; nosotros vamos a necesitar dos. La primera dice que un sistema no puede ocupar el mismo estado en dos movimientos distintos. En román paladino: dos líneas rojas no se pueden cortar bajo ningún concepto en ningún punto. La explicación hay que buscarla en una propiedad especial (y muy útil) de las ecuaciones de Hamilton: su solución es única para cada condición inicial, luego no ha lugar a que dos evoluciones distintas del sistema tengan un estado en común. "¡Espere, profesor!" Otra vez interrumpiendo, ¿pequeño Timmy? "Sí, profesor, porque eso que ha dicho está mal. ¿Ve ahí, en el dibujo de la derecha, como sí se tocan dos trayectorias distintas en pi y -pi?" ¡Oh! Muy observador, pequeñajo, pero me temo que has caído en una ilusión óptica. No me mires con esa cara, pues es un error muy común. Lo que sucede en realidad es que para esa trayectoria el péndulo tiene un periodo... ¡infinito! Así, por mucho que uno espere, un péndulo simple con velocidad nula y posición pi nunca llegará a terminar su oscilación; necesitarías ampliar infinitamente la escala en ese punto para ver el ansiado corte. La segunda regla inquebrantable es aún más robusta porque es un teorema válido para nuestro sistema clásico. El teorema de Liouville establece que el volumen del espacio de fases ocupado por un sistema se mantiene constante a lo largo de una evolución temporal. En un gas como el nuestro, el volumen que ocupase el conjunto de puntos representando el estado de cada una de las partículas debe ser el mismo tanto en el estado inicial como en el final y en todos los intermedios, sin importar la forma que deba adoptar para conservar esta magnitud (valga la figura siguiente como ejemplo extremo).

Pasemos a hablar de los estados, o sea, cada uno de los puntos del espacio de fases. Cuando el diablillo separa las partículas del gas según su velocidad está llevando al gas a una situación menos favorable que el reparto homogéneo. Para el gas resulta más cómodo tener sus partículas repartidas uniformemente que separadas según sus velocidades; se conoce a estas situaciones como estados de equilibrio. Estos no son ni mucho menos únicos; existen numerosas velocidades que cada partícula del gas puede de manera que el conjunto se mantenga en equilibrio. A cada una de las distintas configuraciones que puede tener un estado se la conoce como microestado. Los estados de equilibrio del gas se caracterizan por tener millones y millones y millones... de microestados más que los estados de no-equilibrio, haciendo que la inmensa mayoría de los puntos del espacio de fases sean configuraciones de equilibrio (el volumen que suman todos esos puntos es mucho mayor que aquél que suman los de no-equilibrio). En nuestro caso, los estados de no-equilibrio se encuentran en la región transitoria entre el comienzo y el final de la acción del diablillo.

Si has llegado hasta aquí, ¡enhorabuena! Ahora te queda reposarlo tranquilamente y releerlo tantas veces como quieras porque ya tienes las herramientas suficientes para afrontar la prueba del algodón: ¿puede existir el diablillo de Maxwell en la realidad? La semana que viene, queridos diablillos, afrontaremos la batalla final. A continuación te dejo con un caso particular en el espacio de fases donde trabajar algunos de los conceptos previos.

EXTRA: una vuelta de tuerca al péndulo simple

Para los aventureros, aquí va un caso sencillo del que podemos extraer mucha chicha. Sea el hamiltoniano de un péndulo simple unidimensional:

donde omega representa la frecuencia angular (2pi/periodo). Sus ecuaciones de movimiento (extraídas a partir de las de Hamilton) son:

Imponiendo que en el instante inicial la posición es una cantidad a y su momento lineal es nulo se obtienen las soluciones :

¿Cómo se ve en el espacio de fases? Una de las trayectorias es la siguiente:

Una elipse que recorre en sentido horario debido al signo negativo en la expresión del momento lineal. Sin embargo, cabría preguntarnos qué pasaría si cambiásemos las coordenadas del sistema. ¿Qué pasaría si en lugar de mirar el péndulo por su posición y su momento lineal lo hiciéramos en función de otras variables? La mecánica hamiltoniana permite trabajar en los sistemas con variables no "naturales" sin afectar al entendimiento de los sistemas en sí, tan sólo para ofrecer un punto de vista diferente. La libertad de cambios de variable que ofrece la mecánica hamiltoniana fue la clave de su éxito. Ahora bien, no todas las variables valen; se debe cumplir una condición que sólo voy a mencionar aquí: el corchete de Poisson de las dos variables debe ser igual a 1 (se dice que ambas variables son canónicamente conjugadas). Para nuestro caso, la cantidad definida como

donde A es el área de la elipse conmuta con el ángulo o fase girado en la trayectoria del sistema por la elipse (la magnitud que aparecía dentro de las expresiones seno/coseno más arriba). Aplicando la ley de cambio de hamiltonianos, podemos reemplazar el hamiltoniano de la primera ecuación por este nuevo mucho más sencillo

de manera que las ecuaciones de movimiento quedan (agárrate):

¡Si es que parece magia! Pero ahora sí que vas a flipar. En el espacio de fases, el movimiento se ve como:

¡SON RECTAS! ¿No te parece increíble lo que hemos hecho? Aunque me haya saltado algún paso intermedio quiero remarcar que todo lo hecho aquí es legal y representa tan sólo una mínima parte de la potencia del formalismo hamiltoniano. Quizás esto te haya ayudado a comprender un poco mejor por qué insistí tanto en que este método acabó por conquistar el panorama de la física del siglo XIX y XX. Es verdaderamente fabuloso.